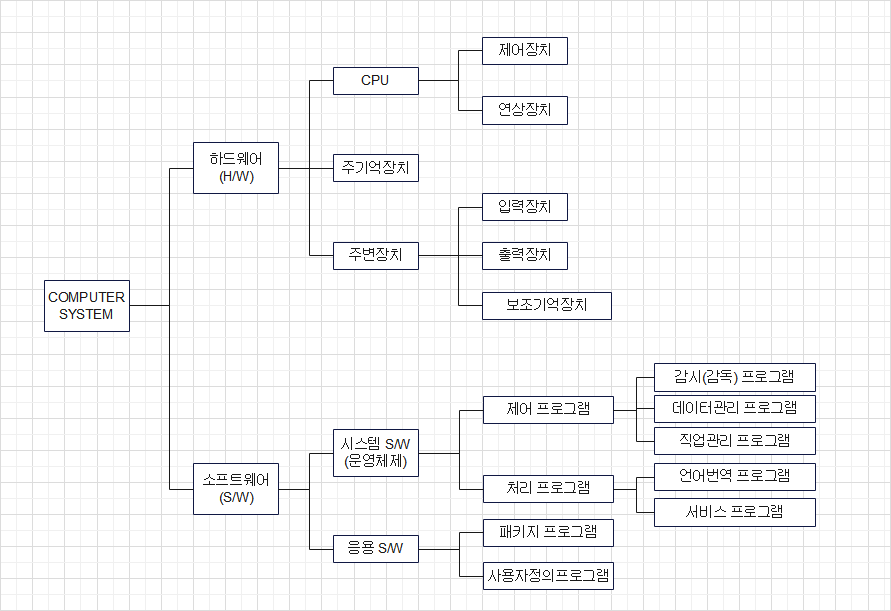
자료의 구성
비트(Bit)
자료표현의 최소단위로 Binary digit의 약어임
비트는 0과 1로 표현되는 2진수 한자리를 기억시킬 수 있는 기억공간
니블(Nibble)
4비트로 10진수 한자리를 표현하는 단위로 사용 됨
바이트(Byte)
8비트로 문자표현의 최소단위
워드(Word)
CPU에서 처리되는 명령의 단위, half word = 2byte, full word = 4 byte, double word = 8byte로 나뉨
자료 연산 단위로 한번에 처리할 수 있는 자료의 양
64비트 컴퓨터라면 한번에 64비트씩 처리할 수 있는 능력을 가짐
필드(Field) 또는 항목(Item)
레코드를 구성하는 항목으로 파일(File)을 구성하는 단위 중 최소의 논리적 단위
레코드(Record)
서로 관련된 필드 또는 항목의 집합으로 프로그램 상에서 자료의 처리 및 기록의 단위 -> 논리적 단위, 내부에서 처리되는 단위
필드의 집합으로 데이터베이스에서 실제로 정보를 처리할 때 기본이 되는 단위
파일(File)
구조가 같은 레코드의 집합으로 기억매체에 저장되는 단위
데이터베이스(Database)
여러 응용분야에서 여러 사람들이 공동으로 사용할 수 있도록 조직, 관리되고 있는 자료의 모임
진법 변환
10진법 : 0, 1, 2, … , 9로 표현되는 10개의 digit로 숫자를 표현
2진법 : 0, 1로 표현되는 2개의 digit로 숫자를 표현
8진법 : 0, 1, 2, … , 7로 표현되는 8개의 digit로 숫자를 표현
16진법 : 0, 1, 2, … , 9, A, B, C, …, E, F로 표현되는 16개의 digit로 숫자를 표현
10진수의 다른진수 변환
정수의 변환 : 10진수를 해당 진수로 나누어 몫은 그대로 두고, 나머지를 해당 진수의 마지막 자리로 취하는 과정을 몫이 진수보다 작아질때까지 반복
소수의 변환 : 10진수를 변환시킬 진수로 곱한 다음, 계산된 결과의 정수 부분을 제외하고, 소수 부분이 0이 되거나 반복되는 수가 나올때까지 곱하기를 반복
자료의 표현
수치자료
┣ 정수표현(고정소수점 수의 표현)
│ ┣ 10진연산
│ │ ┣ 언팩연산
│ │ └ 팩연산
│ └ 2진연산
│ ┣ 부호화크기
│ ┣ 1의 보수
│ └ 2의 보수
└ 실수표현(부동소수점 수의 표현)
문자자료
┣ BCD code : 2진화 10진 코드
┣ EBCDIC code : 확장된 2진화 10진 코드
└ ASCll code : 정보교환 미국표준코드
수치자료 – 정수표현(고정소수점 수의 표현)
10진 연산
언팩형식
10진수 한 자리를 한 바이트로 표현(존 4비트와 숫자 4비트 사용)
최하위 바이트의 존부분을 부호로 사용
16진수로 표현하며, C(1100)은 양수, D(1101)은 음수, F(1111)은 부호없음을 의미함

팩형식
10진수 한 자리를 4비트로 표현
1바이트에 2개의 숫자 표현 가능
최하위 4비트를 부호로 사용하며 표현형식은 언팩형식과 동일

2진 연산
2진법으로 표시되는 정수는 부호 비트 부분과 크기 표시 부분으로 나뉨
2진연산은 부호화 크기, 1의 보수, 2의 보수 방식으로 구분
보수를 이용하면 뺄셈이 덧셈의 원리로 연산이 가능하며, 감산기 필요없이 가산기로 모든 사칙연산이 가능 함
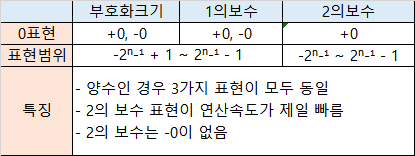
부호화크기(Signed Magnitude)
MSB(Most Significant Bit)를 부호 비트로 두어 MSB가 0이면 양수, 1이면 음수를 나타냄
음수표현이 간단하지만, 가.감산기가 모두 필요하여 HW비용이 증가함
수 표현범위 : -2n-1 + 1 ~ 2n-1 – 1
1의 보수(1’s Complement)
음수 표현시 0은 1로 1은 0으로 바꿈
덧셈할때 윤환 올림수(end around carry)가 발생할 수 있는데, 1의 보수를 이용하면 연산시 윤환 올림수 처리과정이 필요
수 표현범위 : -2n-1 + 1 ~ 2n-1 – 1
2의 보수(2’s Complement)
1의 보수에 1을 더하여 음수를 표현
다른 두 방식에서 +0과 -0이 표현되는것을 0 하나의 표현으로 해결함
수 표현범위 : -2n-1 ~ 2n-1 – 1
장점으로는 0이 하나, 다른 방식보다 음수 하나를 더 표현 가능, 윤환 올림수 연산과정 필요없음, 연산속도 빠름 등이 있음
수치자료 – 실수표현(부동소수점 수의 표현)
2진 실수 데이터 표현과 연산에 사용
하나의 수를 고정 소수점 부분을 나타내는 부분(가수)과 고정 소수점 위치를 나타내는 부분(지수)으로 나누어 표현하는 표기법
정밀도를 요구하는 과학, 기술 계산에 적합함
지수부가 클수록 더 큰 수나 더 작은 수를 표현할 수 있으며, 가수부를 크게 할수록 정밀도가 증가함
정규화된 표현의 경우 2진 소수점 앞의 첫번째 비트는 항상 1이 되기 때문에 이 비트를 저장할 필요는 없고 후에 그 수를 이용한 산술 계산과정에서 그 비트가 있는 것으로 처리해주면 됨
정규화(normalize)는 소수점을 이동하여 소수 첫째 자리에 유효 숫자가 오도록하여 지수부 + 가수부의 형태로 만드는 것으로 연산속도를 느리게 함
IEEE 754 표준 부동소수점 수의 형식
IEEE(국제 전기 전자 기술자협회)에서 표준을 제안 함
지수부가 모두 0인 경우 언더플로, 반대로 모두 1인 경우는 오버플로이거나 무한대 값을 표현하는데 예약되어 사용가능함
8비드 지수를 가지는 32비트 단정도(signle-precision) 형식과 11비트 지수를 가지는 64비트 배정도(double-precision) 형식을 정의하고 있으며, 기수는 2임


IEEE표준은 1.M X 2E의 형태를 가지며, 소수점 좌측의 1은 감추어지고 소수점 아래의 M 부분만 가수 필드에 실제로 표현됨
N = (-1)SM X BE
* S:수의부호(양수 0, 음수 1), M:가수, B:기수, E:지수
지수 필드는 바이어스 된 2진수로 표현되며, 바이어스 값은 127
ex) 10진수 N = -13.625를 부동소수점 형식으로 표현(bias 127)
-13.625 = -1101.101 = -1.101101 X 23
부호(S)는 음수(1)
지수(E)는 01111111(bias) + 00000011 = 10000010
가수(M)는 (1.)10110100000000000000000
S E M
결과 : 1 / 10000010 / 10110100000000000000000
N = (-1)1*2130-127*1.101101 = -(1101.101)2 = -13.625
문자 자료 표현
BCD(Binary Coded Decimal) 코드
BCD코드는 8421코드, 2진화 10진 코드라고도 함
6비트로 구성(zone : 2bit, digit : 4bit), 26(64)개의 문자 표현이 가능함
영문 대.소문자를 구별하지 못함


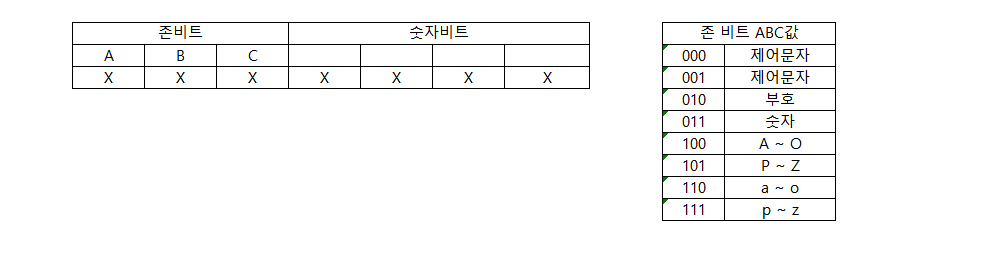
EBCDIC(Extended Binary-Coded Decimal Interchage code) 코드
8bit로 구성(zone : 4bit, digit : 4bit)되어 28(256)개의 문자 표현이 가능
EBCDIC(엡씨딕, 확장된 2진화 10진 코드)코드는 BCD 코드에 2개의 Bit를 추가
주로 IBM 컴퓨터에서 사용


ASCll(American Standard Code for Information Interchange) 코드
ASCll 코드는 ISO에서 개발되어 ANSI(American National Standards Institute)에 의해서 제정된 데이터 전송표준코드
각각의 알파벳이나 숫자 그리고 특수문자들이 7비트(zone : 3bit, digit : 4bit)의 2진수로 표현되며, 27(128)개의 문자표현이 가능
데이터 통신용이나 마이크로컴퓨터에서 사용

Unicode
Unicode는 국제표준으로 제정된 2바이트계의 만국 공통의 국제 문자부호 체계(UCS : Universal Code System)이며, 데이터의 교환을 원활하게 하기 위하여 문자 1개에 부여되는 값을 16비트로 통일함
텍스트나 스크립트 문자에 대한 바이너리 코드를 확립하기 위한 새로운 아이디어로 24개 언어를 지원하기 위해 34,168개의 개별 코드문자를 담고있는데, 이 문자들은 세계 주요 언어로 작성된 문자들을 모두 충족시키기에 충분하며, 심지어 여러가지 언어로 작성된 고문서까지도 지원 가능함
기타코드
가중치(Weighted) 코드
각 자릿수에 고유한 가중치를 가진 코드
종류는 2421코드, 51111코드, 7421코드, 74-2-1코드, 8421코드, 84-2-1코드, Biquinary(5043210)코드, 링카운터(9876543210)코드 등이 있음
비가중치(Unweighted) 코드
각 자릿수에 가중치를 가지지 않는 코드
종류는 3초과 코드, 그레이코드, 2 out of 5 코드(5중 2코드), 3 out of 5 코드(5중3코드)등이 있음
오류 검출 코드
오류를 검출할 수 있는 코드
종류는 패리티 검사 코드, 해밍 코드, 2 out of 5 코드(5중 2코드), 3 out of 5 코드(5중 3코드), 바이퀴너리 코드, 링카운터 코드 등이 있음
자보수 코드
어떤 코드의 1의 보수를 취한 값이 10진수의 9의 보수인 코드
종류는 3초과코드, 2421코드, 51111코드 , 84-2-1코드 등이 있음
그레이(Gray) 코드
연속된 코드가 한 비트만의 변화로 새로운 코드를 순차적으로 생성함
XOR원리를 이용한 비가중치(Non-Weighted) 코드로 연산이 불가능
입출력장치 코드, A/D 변환기(Analog-to-Digital Converter) 등에 사용
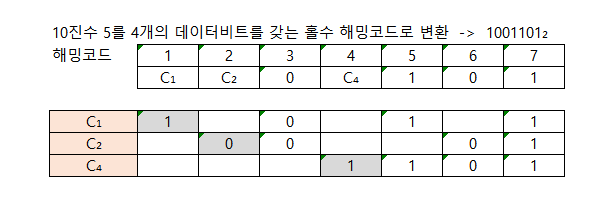
해밍(Hamming) 코드
8421코드에 3비트의 패리티 비트를 추가해서 구성하며, 오류의 발견은 물론이고 교정까지 할 수 있음
두 비트가 동시에 바뀌는 경우 오류를 검출할 수 없다는 단점이 있음
패리티 비트의 위치는 2n(n=0,1,2,3,…) 즉, 1,2,4,8,…번째
연산의 종류
자료 성질에 따른 분류
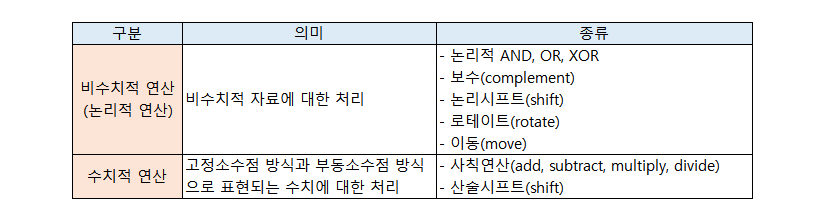
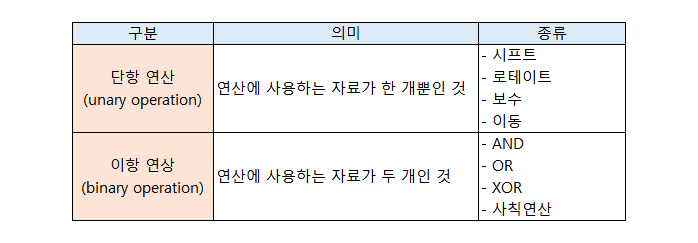
자료 수에 따른 분류
이전게시글

다음게시글