컴퓨터의 발전과정
| 순서 | 고안자 | 설명 | 특징 |
| 에니악(ENIAC, 1946) | 에커트 | 진공관으로 연결된 외부 프로그래밍 방식 | 최초의 컴퓨터, 10진법 사용 |
| 에니삭(ENSAC, 1949) | 윌키스, 모리스 | 폰노이만의 프로그램 내장방식 채택 | 최초의 프로그램 내장방식 |
| 에드박(EDVAC, 1950) | 모클리, 에커트 | 프로그램 내장방식 완성 | 최초의 2진법 사용 |
| 유니박(UNIVAC, 1951) | 모클리, 에커트 | 미국 인구 통계에 이용, 자기테이프 사용 | 최초의 상업용 컴퓨터 |
| 알테어(1975) | MITS사 | 스위치 조작으로 프로그래밍 | 최초의 개인용 컴퓨터 |
| 애플II | 애플사 | 현재 PC의 형태를 갖춤 | 최초의 8비트 개인용 컴퓨터 |
컴퓨터의 분류
사용목적에 따른 분류
범용컴퓨터(General Purpose Computer) : 일반적으로 사용하는 컴퓨터
전용컴퓨터(Special Purpose Computer) : 전문적으로 사용되는 특수용 컴퓨터로 군사용, 항공산업, 의료용 등으로 이용
데이터 취급 방법에 따른 분류
아날로그 컴퓨터, 디지털 컴퓨터, 하이브리드 컴퓨터로 분류
컴퓨터의 세대별 분류
| 1세대 | 2세대 | 3세대 | 4세대 | 5세대 | |
| 주요 소자 | 진공관(Tube) | 트랜지스터(TR) | 집적회로(IC) | 고밀도집적회로(LSI, VLSI) | 광소자(ULSI) |
| 연산 속도 | ㎳(10-3) | ㎲(10-6) | ㎱(10-9) | ㎰(10-12) | fs(10-15) |
| 기억장치 | 수은지연 회로 | 자기코어 | 반도체 | 반도체 | 반도체 |
| 사용 언어 | 저급언어(기계어, 어셈블리어) | 고급업어(Fortran, Cobol) | 구조적 언어(Pascal, C언어) | 비절차적 언어(SQL) 객체지향언어 | AI, 자연어, 패턴인식 |
| 주요 특징 | 하드웨어 중심 일괄처리시스템 | 다중 프로그래밍 시분할/실시간 시스템 가상기억장치 | UNIX 소프트웨어공학 다중(혼합)모드시스템 | 분산처리 시스템 개인용 컴퓨터 가상기계 병렬처리 시스템 | 지식기반 시스템 전문가 시스템 |
집적회로(IC)
두께가 얇은 실리콘 원판으로 만들며, 웨이퍼라고 함
집적회로는 하나의 반도체 웨이퍼 위에 수백만개의 미세한 저항, 콘덴서, 트렌지스터, 다이오드 등이 만들어져 있고 집적회로 또는 마이크로칩이라고 함
| 칩 종류 | 집적된 수 |
| SSI(Small Scale Integration) | 100개 미만 |
| MSI(Medium Scale Intergration) | 100 ~ 1,000개 |
| LSI(Large Scale Intergration) | 1,000 ~ 100,000개 |
| VLSI(Very Large Scale Integration) | 100,000 ~ 1,000,000개 |
| ULSI(Ultra Large Scale Integration) | 1,000,000개 이상 |
표현단위
| 연산속도 | 기억용량 | |
| 단위 | ms(밀리/초 : milli second) : 10-3 | 1KB(Kilo Byte)=210(103)Byte |
| ㎲(마이크로/초 : micro second) : 10-6 | 1MB(Mega Byte)=220(106)Byte | |
| ns(나노/초 : nano second) : 10-9 | 1GB(Giga Byte)=230(109)Byte | |
| ps(피코/초 : pico second) : 10-12 | 1TB(Tera Byte)=240(1012)Byte | |
| fs(펨토/초 : femto second) : 10-15 | 1PB(Peta Byte)=250(1015)Byte | |
| as(아토/초 : atto second) : 10-18 | 1EB(Exa Byte)=260(1018)Byte | |
| 1ZB(Zetta Byte)=270(1021)Byte | ||
| 1YB(Yota Byte)=280(1024)Byte |
부울대수(Boolean Algebra)
하나의 명제가 참 또는 거짓인가를 판단하는데 이용되는 수학적인 방법으로 수학자 불(G.Boole)에 의해 개발됐으며,
변수 사이의 진리표 관계, 논리도의 입출력 관계를 대수형식으로 표시하기 위해 씀
기본법칙
| 기본 법칙 | 내용 |
| 교환 법칙 | A + B = B + A, A · B = B · A |
| 결합 법칙 | (A + B) + C = A + (B + C), (A · B) · C = A · (B · C) |
| 배분 법칙 | A · (B + C) = A · B + A · C, A + (B · C) = (A + B) · (A + C) |
| 부정의 법칙 | (A’)’ = A |
| 누승 법칙 | A + A = A, A · A = A |
| 항등 법칙 | A + 0 = A, A + 1 = 1, A · 1 = A, A · 0 = 0 |
| 보간 법칙 | A’ + A = 1, A’ · A = 0 |
| 흡수 법칙 | A + A · B = A, A · (A + B) = A |
| 드 모르간 (De-Morgan) 법칙 | (A + B)’ = A’ · B’, (A · B)’ = A’ + B’ |
논리식과 진리표
논리 회로에서 입력은 논리변수, 출력은 논리식의 결과임.
따라서 논리식의 의미를 해석하기 위해서는 논리식을 구성하는 각 논리변수의 가능한 모든 논리 값의 조합에 대해 논리식이 가지는 값을 얻어야하므로 진리표를 사용함.
따라서 논리 회로의 설계는 진리표에서 논리식을 구한 다음 논리 회로를 구성함
논리식의 종류
최소항(Minterm) : 논리 변수가 n개일 때, n개의 논리 변수가 모두 포함된 곱항
최대항(Maxterm) : 논리 변수가 n개일 때, n개의 논리 변수가 모두 포함된 합항
| X | Y | Z | 최소항 | 최소항표현 | 최대항 | 최대항표현 |
| 0 | 0 | 0 | X’ Y’ Z’ | m0 | X + Y + Z | M0 |
| 0 | 0 | 1 | X’ Y’ Z | m1 | X + Y + Z’ | M1 |
| 0 | 1 | 0 | X’ Y Z’ | m2 | X + Y’ + Z | M2 |
| 0 | 1 | 1 | X’ Y Z | m3 | X + Y’ + Z’ | M3 |
| 1 | 0 | 0 | X Y’ Z’ | m4 | X’ + Y + Z | M4 |
| 1 | 0 | 1 | X Y’ Z | m5 | X’ + Y + Z’ | M5 |
| 1 | 1 | 0 | X Y Z’ | m6 | X’ + Y’ + Z | M6 |
| 1 | 1 | 1 | X Y Z | m7 | X’ + Y’ + Z’ | M7 |
논리식의 표현
최소항의 합 : 진리표에서 함수 값이 1인 최소항들을 모두 찾아서 OR 연산으로 묶는방법
예시) f1 = x’y’z + xy’z’ + xyz = m1 + m4 + m7 또는 F(x,y,z) = ∑(1.4.7)
최대항의 곱 : 진리표에서 함수 값이 0인 최소항들을 모두 찾아서 AND 연산으로 묶는방법
예시) f1 = (x+y+z)(x+y’+z)(x+y’+z’)(x’+y+z’)(x’+y’+z) = M0M2M3M5M6
또는 F(x,y,z) = ∏(0,2,3,5,6)
* ∑(시그마), ∏(파이,곱)
논리 회로
입력으로 몇개의 펄스를 조합하고, 정해진 조건에 따라 이 조합을 판단하며, 이에 따라 출력을 내는 동작을 논리연산이라 함.
이러한 논리연산을 하는 회로를 논리 회로라 함
이진 정보는 전압신호를 이용하여 0과 1로 표현, 정보처리는 게이트라 불리는 논리회로에서 행해짐
연산 순서는 NOT > AND > OR순으로 진행함
종류
| 게이트 이름 | 기호 | 논리식 | 진리표 |
| AND |  | x = A · B | A B | X ————— 0 0 | 0 0 1 | 0 1 0 | 0 1 1 | 1 |
| OR | 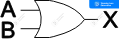 | x = A + B | A B | X ————— 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 1 |
| NOT(inverter) | x = A’ | A | X ———- 0 | 1 1 | 0 | |
| 버퍼(buffer) | x = A | A | X ———- 0 | 0 1 | 1 | |
| NAND | x = (A · B)’ x = A’ + B’ | A B | X ————— 0 0 | 1 0 1 | 1 1 0 | 1 1 1 | 0 | |
| NOR | x = (A + B)’ x = A’ · B’ | A B | X ————— 0 0 | 1 0 1 | 0 1 0 | 0 1 1 | 0 | |
| XOR | x = A ⊕ B x = A’ · B + A · B’ | A B | X ————— 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0 | |
| XNOR | x = (A ⊕ B)’ = A ⊙ B x = A’ · B’ + AB | A B | X ————— 0 0 | 1 0 1 | 0 1 0 | 0 1 1 | 1 |
조합논리회로(Combinational Logic Circuit)
입력신호에 의해서 출력신호가 결정되는 논리회로로 2진 자료를 기억하는 기능은 없으며 논리게이트로 구성됨
종류는 반가산기, 전가산기, 병렬가산기, 반감산기, 전감산기, 디코더, 인코더, 멀티플렉서, 디멀티플렉서, 비교기 등이 있음
반가산기(Half Adder)
자리올림(Carry)은 고려하지 않고 두 비트 A, B만 입력받아 출력에 그의 합 S(sum)와 자리올림수 C0(carry)를 각각 1비트씩 출력하는 회로임
Sum = A’ · B + A · B’ = A ⊕ B
Carry = A · B

전가산기(Full Adder)
자리올림수를 고려한 가산회로, 입력으로 A(더해지는수), B(더하는수), Ci(아랫자리에서의 자리올림)의 3비트를 받아들여 3입력의 합 S(sum)와 윗자리로 올라갈 자리올림(Carry-out) C0를 각각 1 비트씩 출력함
2개의 반가산기와 1개의 OR게이트로 구성
Sum = A’ · B’ · Ci + A’ · B · Ci‘ + A · B’ · Ci‘ + A · B · Ci
= A’ · (B’ · Ci + B · Ci‘) + A · (B’ · Ci‘ + B · Ci)
= A’ · (B ⊕ Ci) + A · (B ⊕ Ci)’ = A ⊕ B ⊕ C
Carry = A’ · B · Ci + A · B’ · Ci + A · B · Ci‘ + A · B · Ci
= Ci · (A’ · B + A · B’) + A · B · (Ci‘ + Ci)
= Ci · (A ⊕ B) + A · B OR A · B + A · Ci + B · Ci

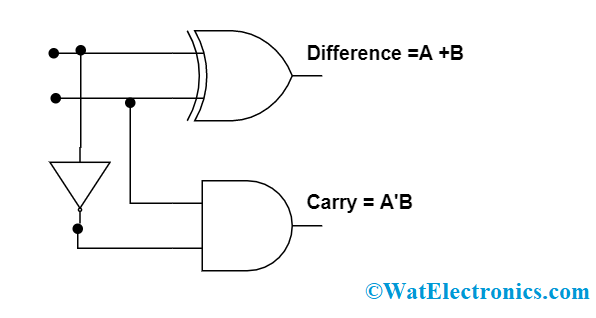
반감산기
X-Y를 계산하여 두 수의 차이 D와 윗자리로부터의 자리 빌림(Borrow) B0를 출력하는 조합논리회로임
계산 과정에서 자리빌림이 발생하면 상위자리로부터 빌림수를 넘겨받거나 하위 자리에 값을 빌려주게 됨
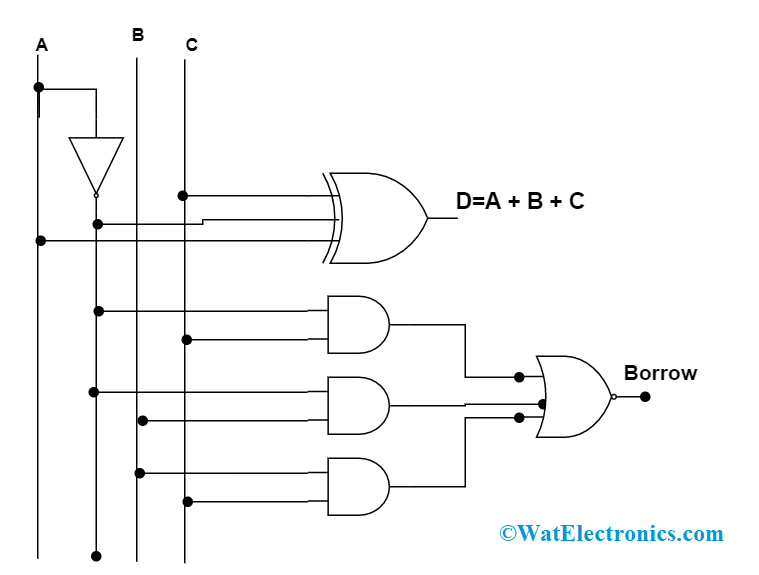
전감산기
아래 자리로 빌려준 자리 빌림(Bi)과 함께 X-Y-Bi를 계산하여 출력 D(차이)와 윗자리로부터 빌려올 자리 빌림 B0를 출력하는 조합논리회로임
두 개의 반감산기와 1개의 OR게이트로 구성
부호기(Encoder)
외부에서 들어오는 임의의 신호를 부호화된 2진 신호로 변환하여 컴퓨터 내부로 들여보내는 디코더와 반대 작용을 하는 조합논리회로임
문자, 숫자, 기호 등을 2진 부호로 변환시킬때 사용 됨
2n개의 입력과 n개의 출력으로 구성(2n X n 인코더) 됨

해독기(Decoder)
부호화된 2진코드를 해독하여 대응하는 하나의 신호를 출력하는 조합논리회로임
ROM, RAM과 같은 기억장치에서 특정한 번지를 선택하거나 명령 레지스터에 들어 온 명령을 해독하는데 사용 됨
n개의 입력과 2n개의 출력으로 구성(n X 2n 디코더) 됨

멀티플렉서(Multiplexer)
2n개의 입력선 중에서 하나를 선택하여 출력선으로 전달하는 회로임
2n개의 입력선 중에서 하나를 선택하기 위한 n개의 선택선이 필요하며, 간단히 MUX라고도 함
디멀티플렉서(Demultiplexer)
1개의 입력신호를 2n개 출력선 중 1개를 선택하여 전달하는 회로임
2n개의 출력선 중에서 하나를 선택하기 위한 n개의 선택선이 필요하며, 간단히 DEMUX라고도 함

순서논리회로(Sequential Logic Circuit)
입력신호와 회로내부의 현상태가 조합논리회로에 의해 출력결과가 결정되는 논리 회로로 2진 자료(0,1)를 기억하는 기능이 있음
순서논리회로는 플립플롭과 논리 게이트로 구성
종류는 플립플롭, 레지스터, 카운터, 동기식 카운터, 시프터 등이 있음
레지스터(Register)
마이크로프로세서의 일부분으로서 아주 작은 데이터를 잠시 저장할 수 있는 공간으로 하나의 명령에서 다른 명령 또는 운영체제가 제어권을 넘긴 다른 프로그램으로 데이터를 전달하기 위한 장소를 제공함
하나의 레지스터는 하나의 명령어를 저장하기에 충분히 커야하지만, 길이가 짧은 명령어를 위한 하프 레지스터라는 작은 레지스터를 쓰기도 함
플립플롭(Flip-Flop)
컴퓨터 내부에서 2진수 ‘0’ 또는 ‘1’의 한 비트를 기억하는 능력을 가진 2진 소자(Cell)이며 이것은 계수기(Computer), 레지스터(Register), 기억소자(Memory Cell)등에 이용 됨플
쌍안정성 회로로 ‘0’ 또는 ‘1’의 상태를 각각 유지하고 있는 두 개의 안정회로임
플립플롭은 두 개의 출력을 갖고 있는데, 이는 항상 보수(Complement) 관계를 갖음
종류는 RS플립플롭, D플립플롭, JK플립플롭, T플립플롭 등이 있음
* 쌍안정성 회로 : 전기적으로 서로 다른 두 정상 상태가 있고 어떤조건의 전기자극에 의해 다른 안정상태로 전이하는 회로
* 보수(Complement) : 각 자리의 숫자의 합이 어느 일정한 수가 되게 하는 수
플립플롭 종류
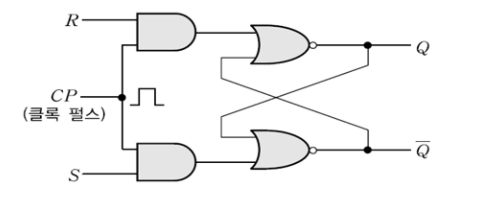
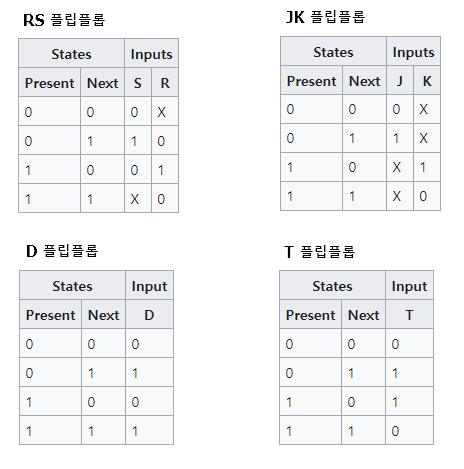
RS 플립플롭
래치(Latch) 회로라고도 하며 Reset단자와 Set단자의 신호에 따라 2진수(0,1) 1자리를 기억하는 플립플롭임
클록펄스(CP; Clock Pulse)에 신호가 들어오지 않으면 S나 R의 입력값에 관계없이 출력값은 변화가 없음
래치 회로는 입력 SR=11을 인가하지 않는다는 조건하에 사용하여야 함
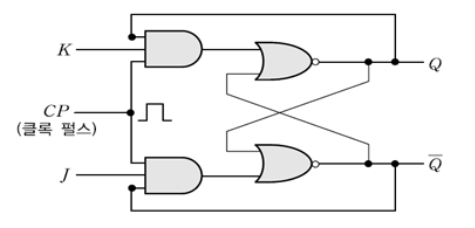
JK 플립플롭
RS플립플롭의 R=S=1일 경우 출력 불안정 상태를 보완한 플립플롭임
RS플립플롭을 개량하여 S와 R에 ‘1’이 동시에 입력되더라도 현재 상태의 반대인 출력으로 바뀌어 안정된 상태를 유지할 수 있도록 한 것임
D플립플롭
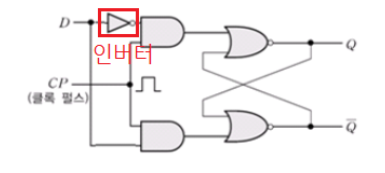
D=0이면 출력은 0, D=1이면 출력은 1이 되며, 출력이 지연(Delay)됨
즉, 신호 D가 그대로 출력 Q에 전달되도록 구성한 회로임
RS플립플롭의 변형으로, R과 S를 인버터(NOT게이트)로 연결함
T플립플롭
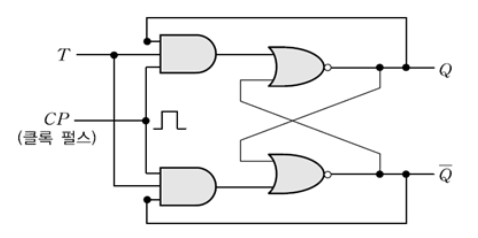
입력 T=0일 경우 JK=00이 되어 출력 Q는 변하지 않게되고, 입력 T=1일 경우 JK=11이 되어 출력 Q값이 반대로 바뀌게 됨
즉, 펄스가 입력되면 현재와 반대의 상태로 바뀌게 되는 토글 상태로 만드는 회로임
JK-FF을 변경시킨 것으로 하나의 입력신호 T를 이용함
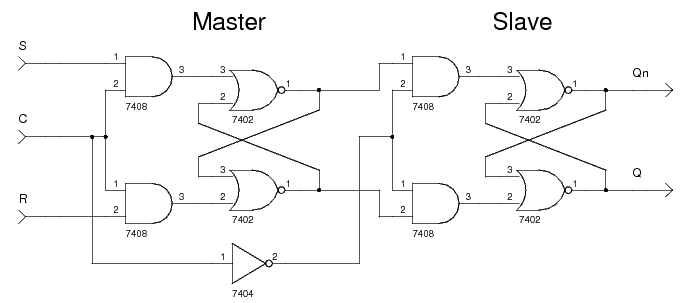
마스터-슬레이브 플립플롭(주종 플립플롭)
JK플립플롭은 J=K=1인 경우 클록이 길면 출력이 계속 반전되는 문제점을 주(Master)와 종(Slave)의 역할을 하는 2개의 독립된 플립플롭을 이용하여 해결함
즉, 마스터-슬레이브 플립플롭은 출력측의 일부가 입력측으로 궤환(Feedback)되어 유발되는 레이스 현상을 없애기 위해 고안된 플립플롭임
여기표(Excitation Table)
플립플롭에서 현재 상태와 다음상태를 알고자할때 플립플롭에 어떤 입력을 넣어야 하는가를 나타내는 표
* X는 0 또는 1을 의미하는 Don’t care의 의미
다음게시글
